假如我们要计算 n 的 15 次方
我们可以很简单的列出以下式子
(1) n^1 * n^1 = n^2
(2) n^2 * n^1 = n^3
...
(14) n^14 * n^1 = n^15
经过 14 次计算后得到
我们也可以有比较聪明的作法
(1) n^1 * n^1 = n^2
(2) n^2 * n^2 = n^4
(3) n^4 * n^4 = n^8
(4) n^8 * n^4 = n^12
(5) n^12 * n^2 = n^14
(6) n^14 * n^1 = n^15
经过 6 次计算后得到
不过我们可以有更聪明的方法
(1) n^1 * n^1 = n^2
(2) n^2 * n^1 = n^3
(3) n^3 * n^3 = n^6
(4) n^6 * n^6 = n^12
(5) n^12 * n^3 = n^15
经过 5 次计算即可得到
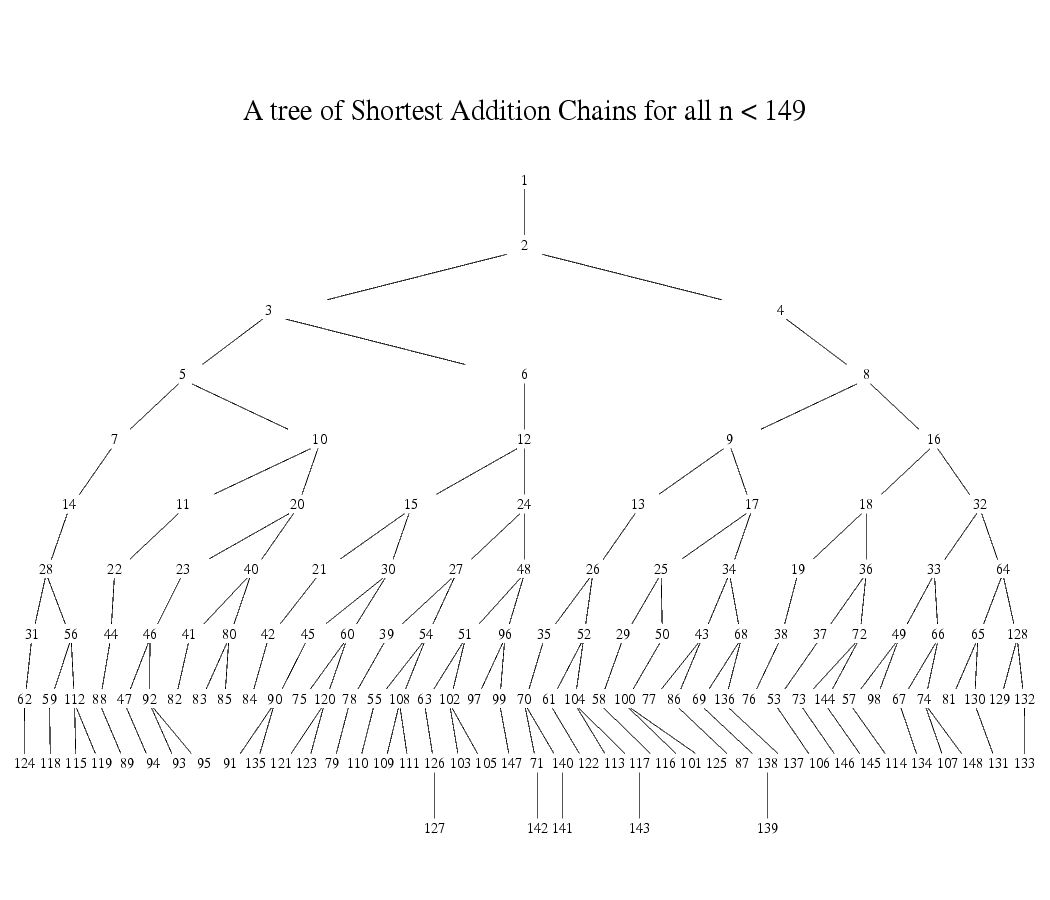
请问: 假如我们要计算 n 的 77 次方
最少需要几次计算? 作法为何?

1,2,4,5,9,18,36,41,77

八次正解 有兴趣的可以去查查看加法链 addition chainshttp://wwwhomes.uni-bielefeld.de/achim/power.gif